Chapter 3 Funktionen

Beispiele und Merkmal von Funktionen

3.1 Grenzwert

\(\lim _ { x \rightarrow 0 } \left( \frac { 1 } { x } \right) = + \infty\)

Durch addition von Werten zu den jeweiligen x und y Werten wird die Orginalfunktion in der jeweiligen Richtung verschoben. Es gilt:

Um einen Funktionsgraph in y-Richtung zu verschieben, muss man eine Zahl a zum Funktionsterm addieren oder subtrahieren.

Eine Verschiebung in x-Richtung erreicht man, indem man x durch x+a oder x−a ersetzt.

Am Beispiel der Funktion \(\frac{1}{x-1}\) wird dies in Bild 3.1 dargestellt

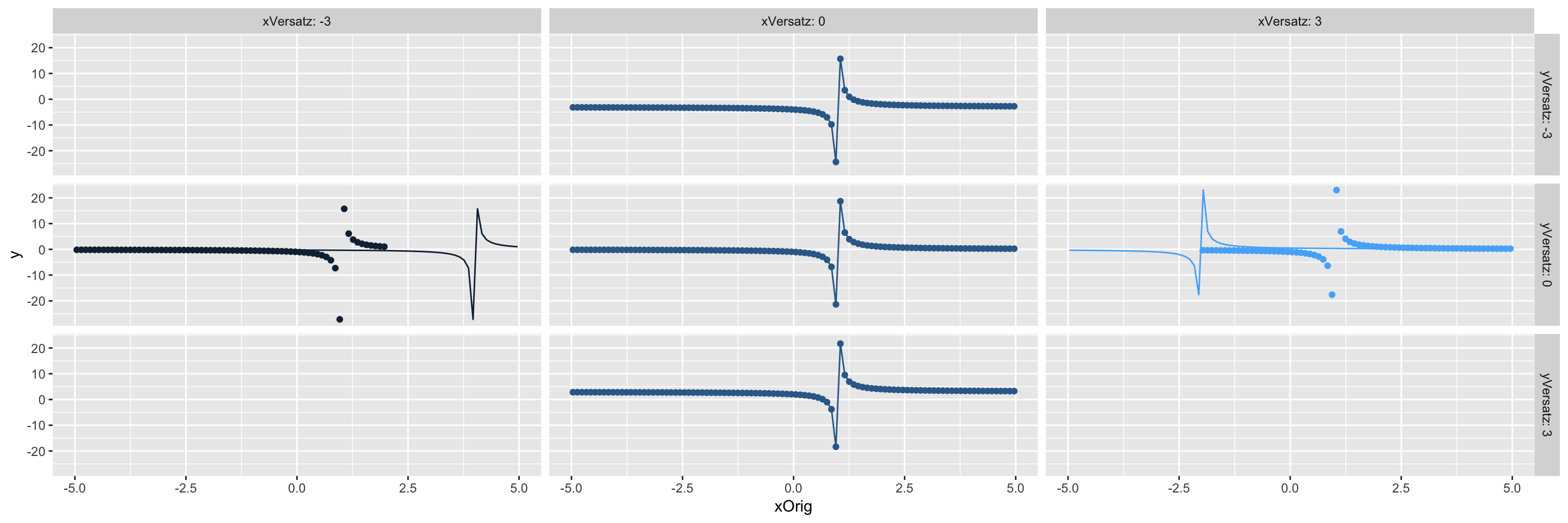
Figure 3.1: Funktion 1/(x-1) verschoben

Ein weiters Beispiel für eine Funktionsverschiebung ist in Bild 3.2 für die Funktion \(x^2+2*x+3\) dargestellt

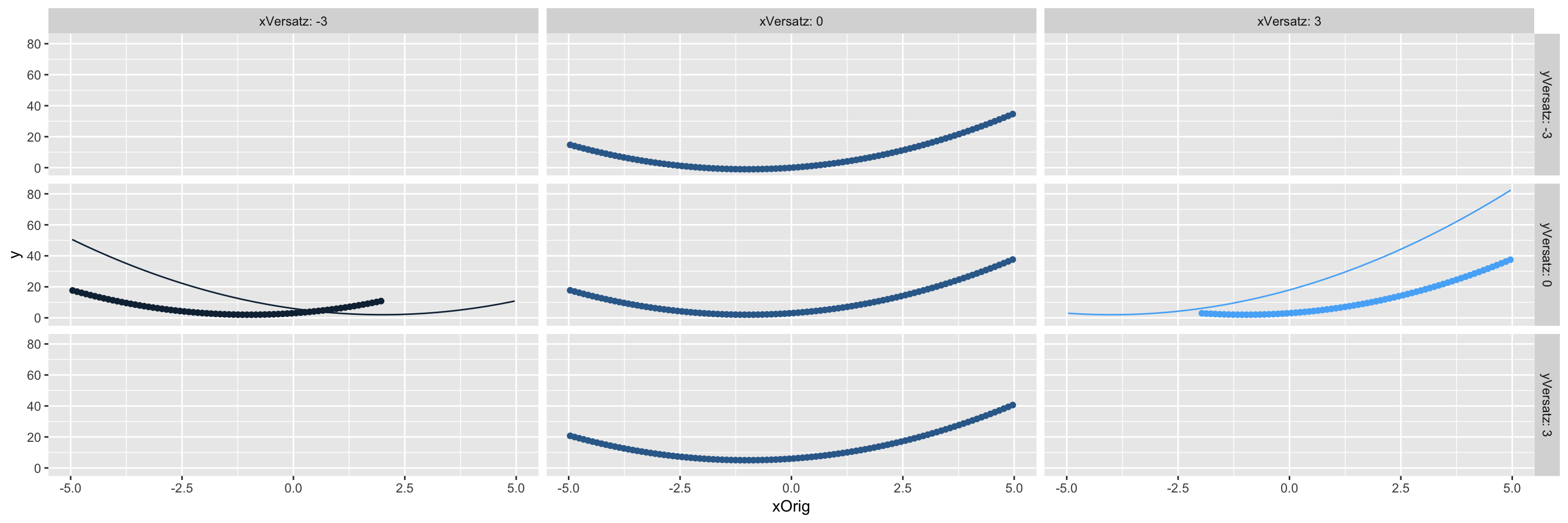
Figure 3.2: Funktion \(x^2+2*x+3\) verschoben

In Bild 3.3 wird in der Orginalfunktion sowohl x als auch y multipliziert. Die Orginalfunktion ist in der Mitte der Plots.

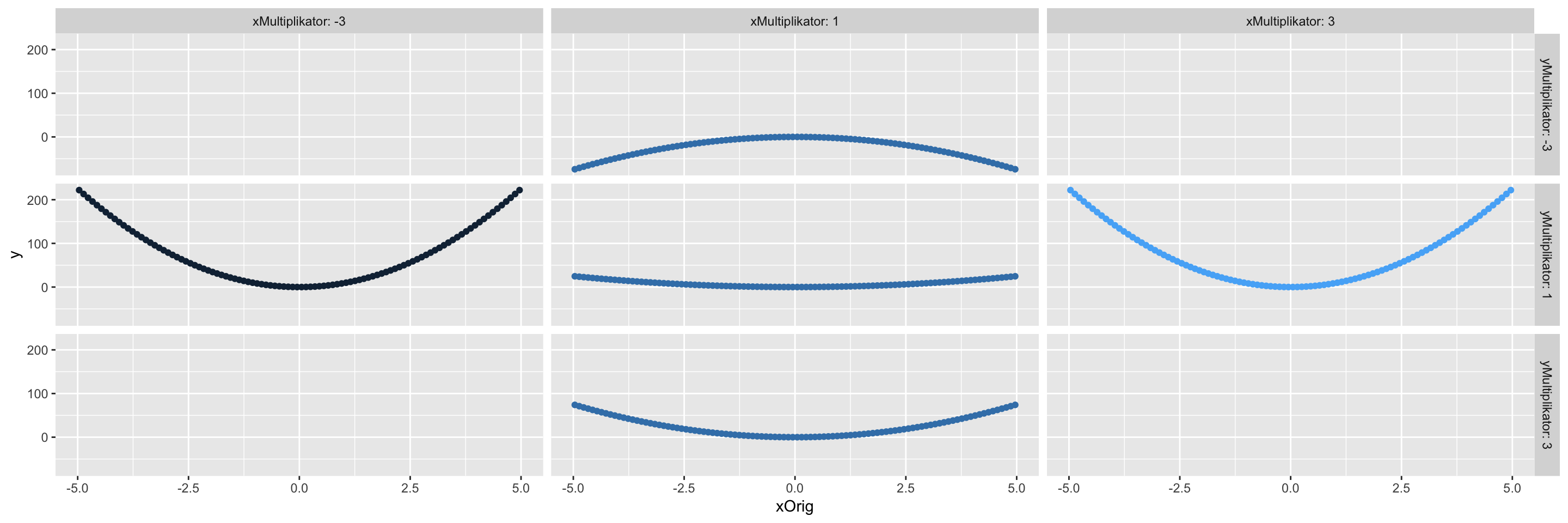
Figure 3.3: Funktion in x und y gestreckt und gestaucht

Siehe nachfolgende Mind Map als Gedankenstütze

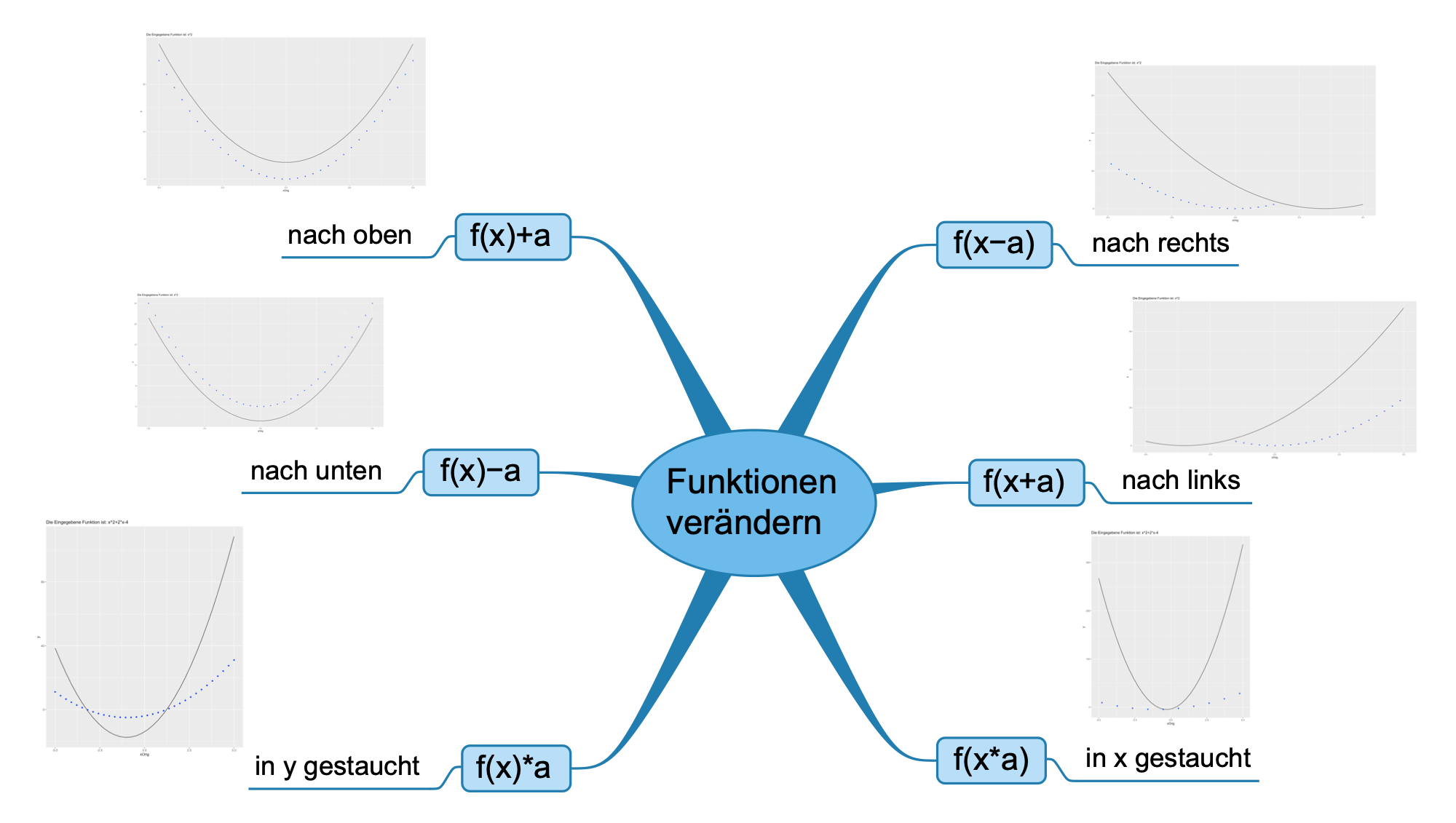
Figure 3.4: Verschiebung durch addtion